考研答疑  |  免费领好课入口

0元下载新手备考资料包包含：历年试题核心词汇政英数热门专业备考思维导图
考研之旅刚刚行程过半，前方仍有复试在等待着大家。为了更好的迎接复试，对今年的考试题目进行分析，有助于合理评估自己的考试分数，为复试复习做好规划。如果发现自己考得不太理想，也可通过分析问题，查漏补缺，整理心情重新出发。
根据考试大纲初等数学部分的要求，管理类综合联考主要考查考生的运用数学基础知识解决问题的方法和能力，具体包括运算能力、逻辑推理能力、空间想象能力和数据处理能力等，对于不同能力考查的题目也是各有特色，基于此我们把整个知识体系分为算术、代数、数据分析、几何及应用题。
代数部分对同学的数学逻辑思维能力有较高要求，在初数中属于难度高、题量大的一个部分，在代数这一模块，主要有六部分知识：整式，分式及其运算、函数、代数方程，不等式，数列、等差数列、等比数列。接下来老师就带着大家把今年初数的代数部分进行分析研究，梳理一下重难点。
（一）考试大纲
1. 整式
（1）整式及其运算
（2）整式的因式与因式分解
2. 分式及其运算
3. 函数
（1）集合
（2）一元二次函数及其图像
（3）指数函数、对数函数
4. 代数方程
（1）一元一次方程
（2）一元二次方程
（3）二元一次方程组
5. 不等式
（1）不等式的性质
（2）均值不等式
（3）不等式求解
一元一次不等式（组），一元二次不等式，简单绝对值不等式，简单分式不等式。
6. 数列、等差数列、等比数列
（二）历年试题代数部分分布情况

年份	2023	2022	2021	2020	2019	2018	2017	2016	2015	2014
题量	6	6	5	8	5	6	6	7	8	6
占比	24%	24%	20%	32%	20%	24%	24%	28%	32%	24%
难度	★★★★

 
（三）2023试题考查分析

2.一元二次方程

3.均值不等式

4.韦达定理

【知识点】一元二次方程韦达定理
考察了韦达定理的两个公式以及二元二次型的因式分解，难度适中。
5.数列

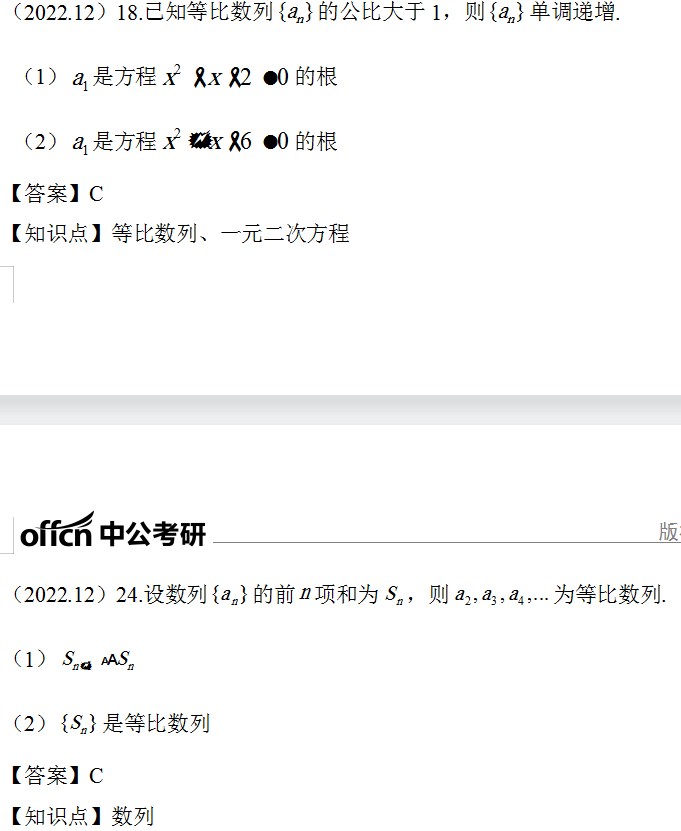
【答案】C
【知识点】数列
数列部分主要考查等比数列的基本公式运用，18题结合了一元二次方程，但计算较为简单，难度不大；24题需要的列式较多，难度较大。
整体来看今年初数题目难度适中，代数部分的考查特点就是题目数量较多，灵活度较强，计算量相对较大，如果综合了其他知识点，题目难度也会随之再次上升，这就是代数部分的难点，但是该部分知识也有优势所在，那就是基础知识点和公式较为固定，只要我们能把平日积累应用于解题过程之中，就可以拿下该部分分数。
对于数学来说，虽然会背公式并不意味着会解题，但是不会公式几乎是无法解题的，所以对于基础知识点以及公式，我们务必要掌握，尤其是代数这一部分。当然，掌握公式只是学好数学的第一步，更重要的是将所学应用于题目之中，题目的练习是必不可少的。
不管最终的结果如何，沿途的风景都是美好的，相信你收获的一定比最开始预想的多，希望你接下来的日子一路生花！

考研实用工具推荐
1、2024考研院校专业匹配查询系统
2、近5年全国各在招院校专业复试分数线查询
3、历年调剂信息查询
4、历年各院校专业目录查询
5、历年各院校报录比查询
6、历年各院校参考书目录查询