
(一)思路
待查找的表必须是有序的,先从中间位置开始比较,比较一次查找的范围便可相应的缩小一半,在缩小的范围中继续折半查找,直到查找成功或失败。
(二)算法
要熟练掌握该算法。设a[]升序有序,有以下算法:
int BinarySearch ( DataType a[], int n, DataType x ){
low = 0; high = n-1;
while ( low <= high ) {
mid = ( low + high )/2; // 折半
if ( a[mid]==x )
return mid; // 找到
else if ( x<a[mid] ) // x位于低半区 [low..mid-1]
high = mid – 1;
else // x位于高半区 [mid+1..high]
low = mid + 1;
}
return -1; // -1表示未找到
}
或者有递归版本:
int BinarySearch ( DataType a[], int low, int high, DataType x ){
if ( low>high ) return -1; // 查找失败
mid = (low+high)/2; // 折半
if ( a[mid]==x )
return mid; // 找到
else if ( x<a[mid] )
return BinarySearch (a, low, mid-1, x);
else
return BinarySearch (a, mid+1, high, x);
}
(三)算法性能分析
1.判定树
判定树是一种描述查找中比较过程的直观形式,每个关键字所在层次就是其查找长度,有利于分析查找过程。折半查找的判定树的叶子结点所在层次之差最多为1,其深度为ëlog2nû+1。
查找过程就是走了一条从根到该结点的路径。
如:表长n=10的有序表,

折半查找的判定树如下:
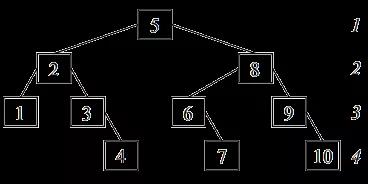
图1 折半查找的判定树
2. 成功的平均查找长度
等概率下查找成功时的平均查找长度:

表长为n=10,平均查找长度如下:

3. 失败的平均查找长度
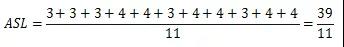
4. 时间复杂度
从平均查找长度看折半查找的时间复杂度是图片。
有时对需要反复查找的数据预先排序,再折半查找也是划算的。
(四)特点
1. 只适用于顺序存储结构,链表无法使用二分查找。
2. 时间复杂度优于顺序查找,但前提是关键字必须有序。
二、往年试卷再现
1. 对序列(2,4,6,8,10,12,14,16,18,20)进行折半查找元素14,需要依次比较( )。
A. 10,18,14
B. 10,16,14
C. 10,18,12,14
D. 10,16,12,14
【答案解析】
1. D。根据折半查找特点,依次比较元素为10、16、12、14,所以选择D选项。考研实用工具推荐
1、2022考研院校专业匹配查询系统
2、近4年全国各在招院校专业复试分数线查询
3、历年调剂信息查询
4、历年各院校专业目录查询
5、历年各院校报录比查询
6、历年各院校参考书目录查询

免责声明:本站所提供的内容均来源于网友提供或网络搜集,由本站编辑整理,仅供个人研究、交流学习使用,不涉及商业盈利目的。如涉及版权问题,请联系本站管理员予以更改或删除。








