2021考研交流群总群
2021考研川师交流群2021在职考研交流群四川考研微信公众号三角形是平面几何中考查的一个重点内容，而三角形的等积模型及其拓展应用是考试中最常考的一个知识点，三角形等积模型包括同底等高、等底等高、等底同高三种最基础的类型，而我们在这里所说的等积模型，是底相等高不相等、高相等底不相等、底和高都不相等的情况下，利用边长的比例关系，转化出两个三角形面积的关系。
在管理类联考中，三角形的这种等积模型面积公式的应用是很常见的，并且考查的难度不低，我们一起来看一下一些三角形等积模型难度较高的拓展应用形式。
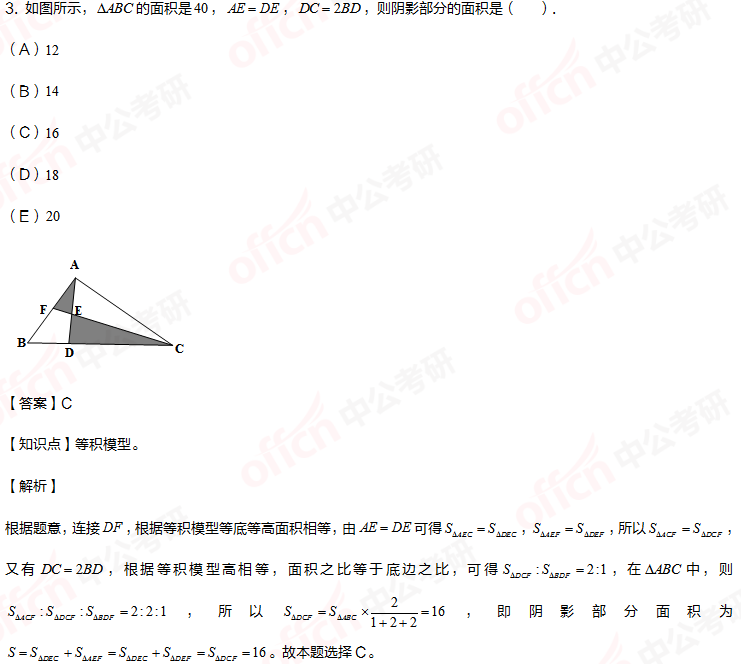
【小结】
这四道题整体思想比较相似，解题的关键在于要能够找出图形中三角形的面积关系，需要将等底等高的三角形做一个等价，把小三角形组合成一个大三角形，从而去求一个三角形的面积即可。
【小结】
本题整体思想是将一个不规则的图形转化成几个比较规则的三角形的面积之和，再分别去求小三角形的面积，之后相加得出所求的面积。
求解图形面积时，我们常使用割补法来将不规则的图形变为规则的三角形来求解面积，在求解三角形面积时，如果题目中没有给出边长的具体值，而是给出一个面积和边长的比例关系，通常要联想到使用等积模型来求解。需要考生掌握的是如何识别等积模型的题目，以及将面积关系转化成边长的比例关系。
四川考研网相关推荐：
阅读全文
免责声明：本站所提供的内容均来源于网友提供或网络搜集，由本站编辑整理，仅供个人研究、交流学习使用，不涉及商业盈利目的。如涉及版权问题，请联系本站管理员予以更改或删除。
