比如练习时有这样的题目：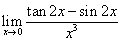

　　有这样的解法：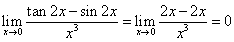

　　从解答过程中可以看出，学生不论前提条件是否满足而生搬硬套地使用等价无穷小替换法则，反映出学生对于该法则的使用没有达到本质的理解。我们知道等价无穷小替换原则是：只能适用于乘除法中，也就是说只能作为乘除因子时才可以使用，而在该题目中，分子中是减法运算不能直接替换，故该方法是错误的。

　　而泰勒公式的好处就是将极限问题化繁为简，即把涉及到的函数全部转化为有理函数。比如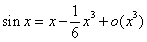，左右两边是等号相连接，只要当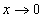时，该式都是成立的都可以使用，比等价无穷小替换使用的范围更广。

　　下面我们结合泰勒公式来重新理解等价无穷小替换的一些法则和原理(假设所有极限中涉及的自变量变化过程都是趋向于零)

　　性质：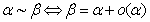

　　我们简单证明一下：若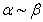，根据等价无穷小的定义可得：，

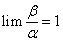　　即：;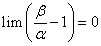

　　;

　　;

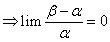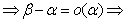
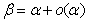　　最初学生对于右边式子中的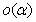会觉得比较抽象难以理解，我们可以结合泰勒公式来形象直观的理解。以正弦函数的泰勒公式为例：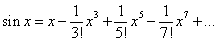

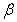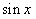　　如果取，那么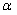可以取x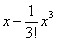，或，或;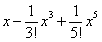

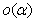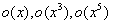　　则：相应的分别为：，所以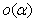并不是抽象的符号，实际代表着具体的表达式，而且该表达式很复杂，由多个式子组成，所以简写成用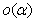来表示。

　　那么在具体的极限题目中，利用泰勒公式具体应该展开到哪一项呢?我们有一个原则就是“上下同阶”。比如在前面的例题中，由于分母是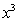，所以我们只展开到第二项就可以了，即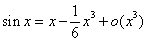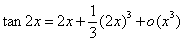：;故上题中正确的作法应为：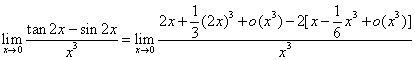

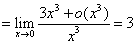
　　所以在求解极限问题的思路中利用泰勒公式比等价无穷小替换法则更一般、更普遍，在解决问题时往往倾向于接受和使用那些放之四海而皆准的思路和方法，关于等价无穷小替换和泰勒公式的使用，同学们要后期多加练习。