
| 2020考研择校择职业指导群 |
| 点击关注“四川中公考研”新浪微博,与博主互动获取考研上名校技巧 |
| 点击关注“四川中公考研”微信公众号,第一时间获取新考研资讯 |
| 一对一择校择职业指导、周末面授班、半年集训、暑期集训营 |
化三角形法是将原行列式化为上(下)三角形行列式或对角形行列式计算的一种方法。这是计算行列式的基本方法重要方法之一。因为利用行列式的定义容易求得上(下)三角形行列式或对角形行列式的性质将行列式化为三角形行列式计算。
原则上,每个行列式都可利用行列式的性质化为三角形行列式。但对于阶数好的行列式,在一般情况下,计算往往较繁。因此,在许多情况下,总是先利用行列式的性质将其作为某种保值变形,再将其化为三角形行列式。

解:首先把第1行分别乘-7、-5、-3,分别加到第2、3、4行上,再交换第2、3行的位置;把第2行分别乘2、-3后,分别加到第3、4行上;后给第行乘1加到第4行。
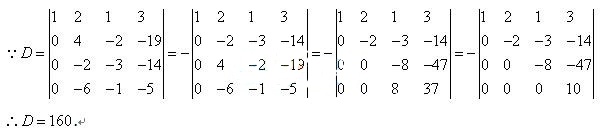
以上是四川中公考研小编为您整理的“2020考研数学线性代数:化三角形法计算行列式 ",预祝每位考生取得好成绩,更多考研常识相关内容尽在四川中公考研数学栏目,中公考研为广大学子推出乐学面授课、VIP一对一等系列备考课程,针对每一个科目要点进行深入的指导分析,欢迎各位考生了解咨询。同时,中公考研一直为大家推出考研直播课堂,足不出户就可以边听课边学习,为大家的考研梦想助力!

免责声明:本站所提供的内容均来源于网友提供或网络搜集,由本站编辑整理,仅供个人研究、交流学习使用,不涉及商业盈利目的。如涉及版权问题,请联系本站管理员予以更改或删除。







