2020计算机考研，关键路径【复习】

　　关键路径算法

　　在AOE网中有些活动可以并行地进行，所以完成工程的最短时间是从开始点到完成点的最长路径的长度(这里所说的路径长度是指路径上各活动持续时间之和，不是路径上弧的数目)路径长度最长的路径叫做关键路径。关键路径上的所有活动都是关键活动(即最迟开始时间等于最早开始时间的活动)。只要找到关键活动，就找到了关键路径。

　　假设：

　　事件(顶点)i：最早发生时间ve(i)，最晚发生时间vl(i);

　　活动(边)a(i，j)：最早开始时间e(i，j)，最晚开始时间l(i，j)。

　　于是，整个工程完工的时间就是终点的最早发生时间。

　　求关键路径的算法步骤：

　　(a)按拓扑有序排列顶点：对顶点拓扑排序;



　　对于关键路径，我们需要注意以下几点：

　　(1)关键路径上的所有活动都是关键活动，它是决定整个工程的关键因素，因此可经过加快关键活动来缩短整个工程的工期。但也不能任意缩短关键活动，因为一旦缩短到一定的程度，该关键活动可能变成非关键活动了。

　　(2)网中的关键路径并不唯一。且对于有几条关键路径的网，只提高一条关键路径上的关键活动速度并不能缩短整个工程的工期，只有加快那些包括在所有关键路径上的关键活动才能达到缩短工期的目的。

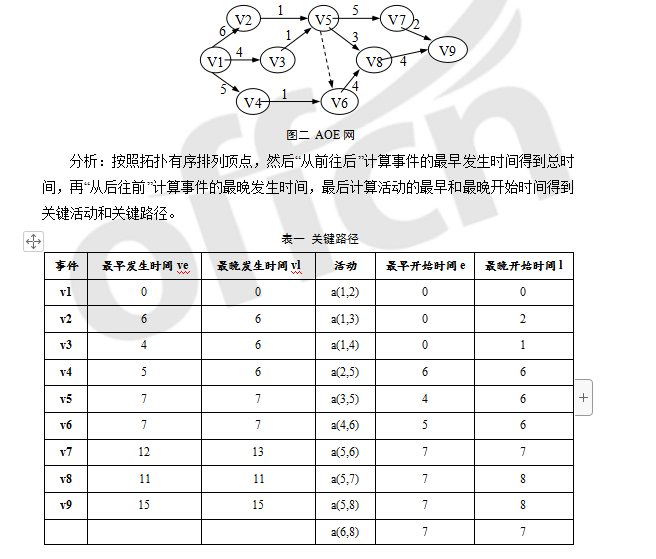
　　例：某工程的AOE网如图二，求(1)整个工程完工需要多长时间，(2)关键路径。说明：图中的虚线仅表示事件的先后关系，不代表具体活动。

　　距离考研越近，有些小伙伴们的心态开始不稳了，压力也感觉越来越大，有的甚至打退堂鼓，太考虑后果只能徒增烦恼，各小伙伴可以提醒自己放平心态，不忘初心，平常心进考场，最后祝大家金榜题名!